Research
These are research I have worked on.
| Title | Description | |
|---|---|---|
|
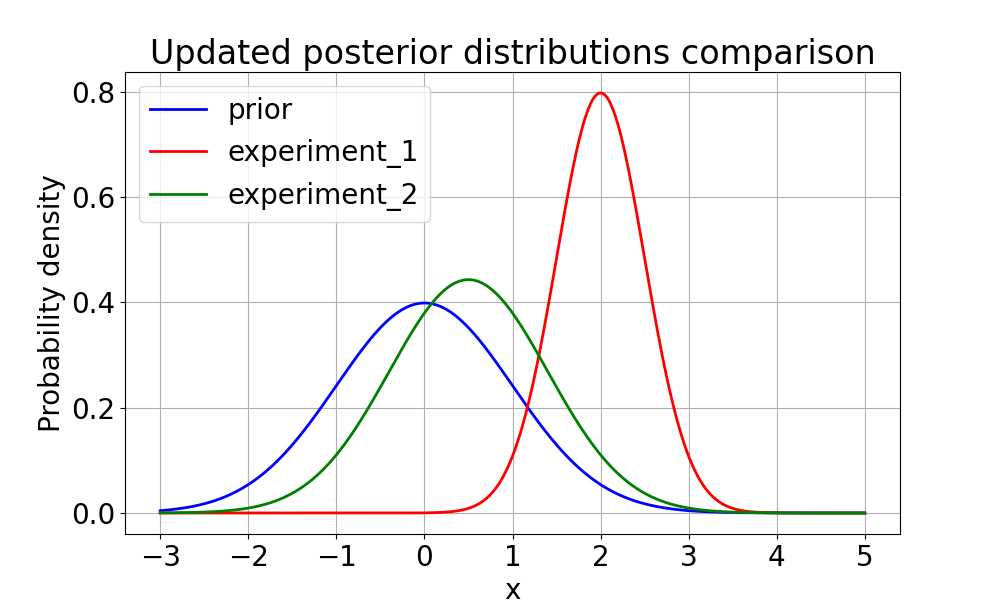
Bayesian Optimal Experimental Design | In research settings where experiments are expensive, time-consuming, or potentially hazardous, it’s crucial to optimize experimental design to maximize information gain. This research advances Bayesian optimal experimental design (BOED) methodology to address these challenges. |
|
|
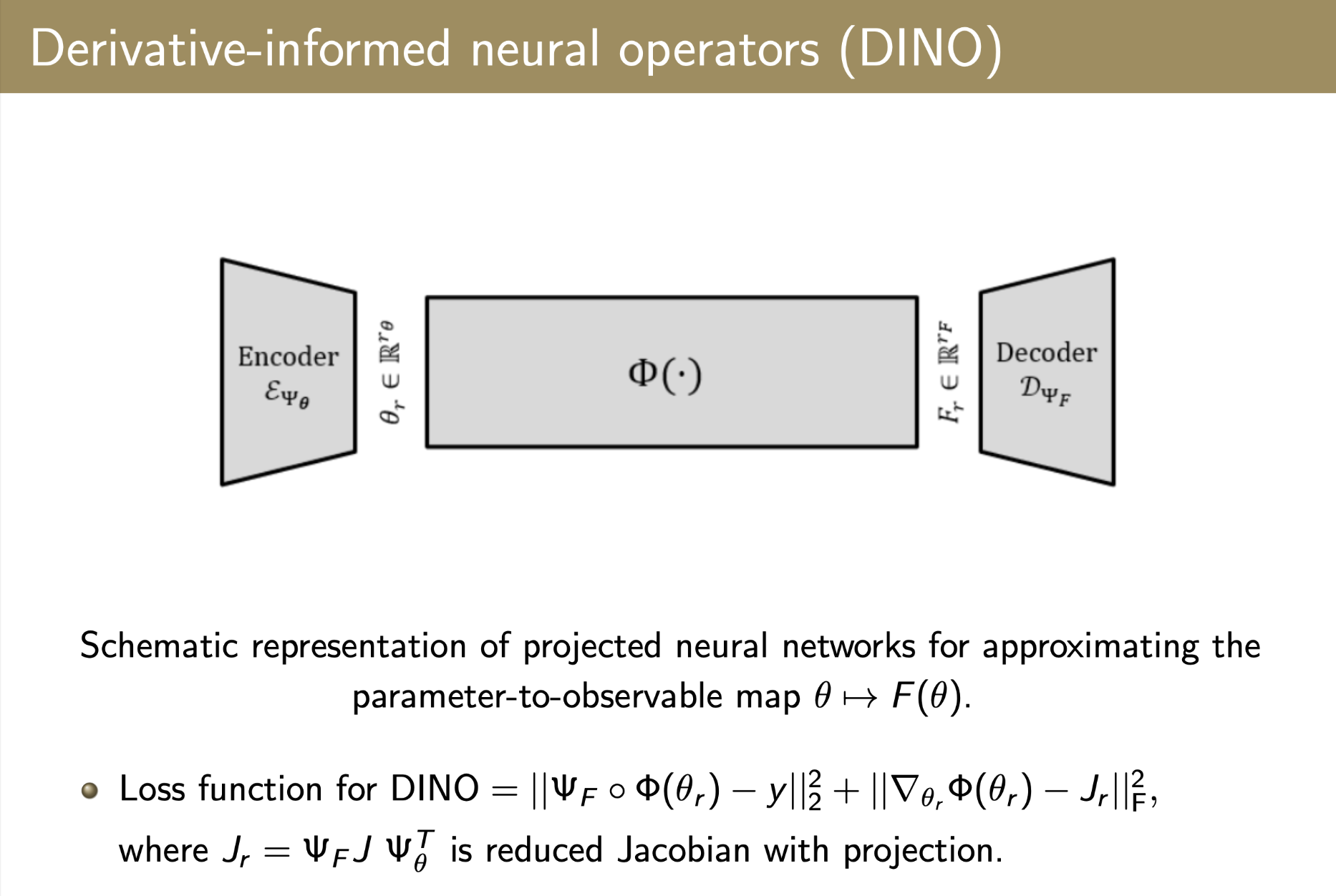
Bayesian Optimal Experimental Design with Neural Operators | Neural operators have emerged as a powerful tool for learning mappings between function spaces, with direct applications to PDEs. These operators provide an elegant solution to reduce the computational burden of infinite/high-dimensional PDE solvers. Through their application in BOED, we’ve developed two approaches: |
|
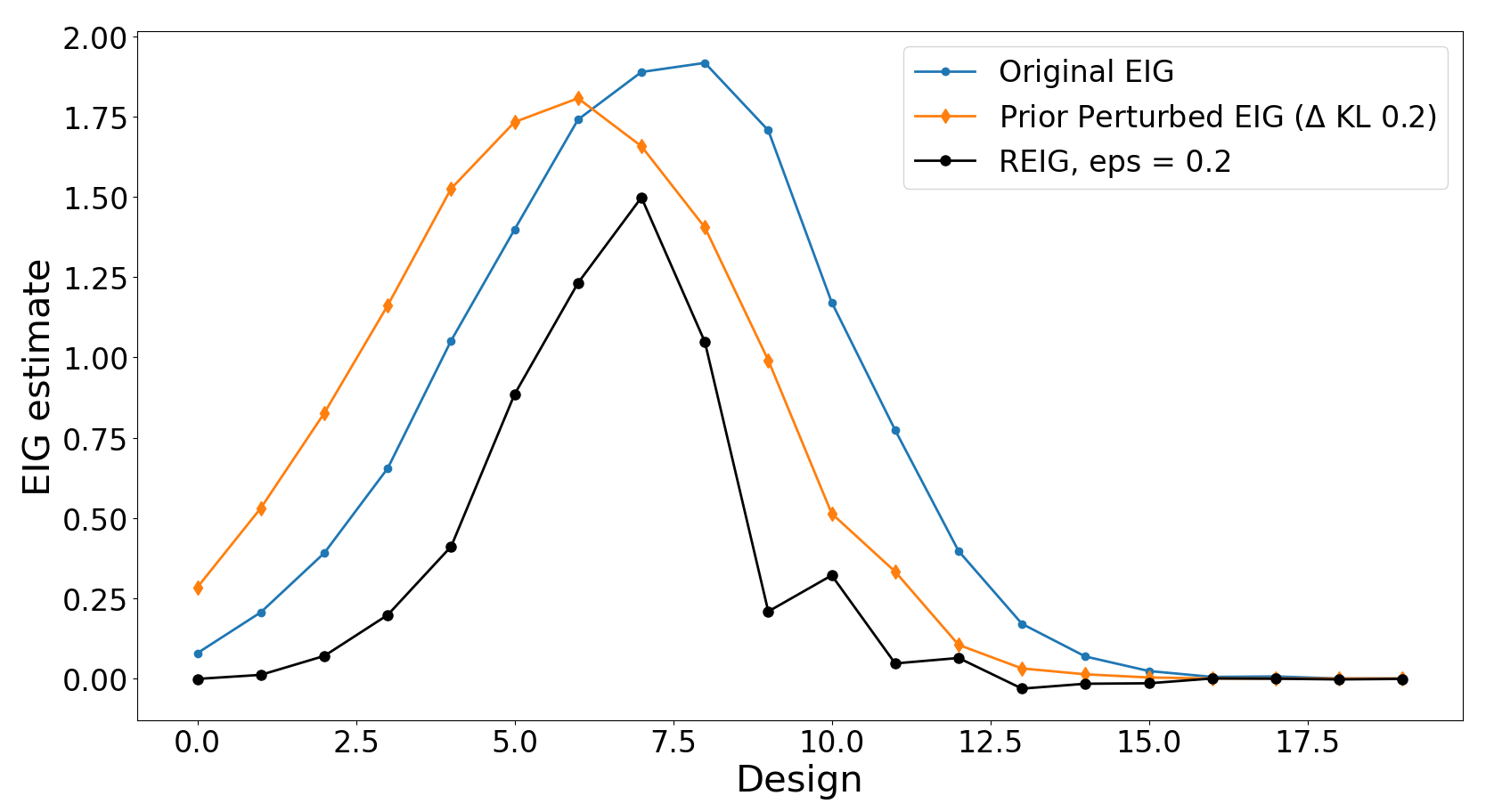
Risk-averse Bayesian Optimal Experimental Design | This project addresses a fundamental challenge in BOED: the sensitivity of experimental outcomes to misspecified prior distributions. While traditional BOED methods assume accurate prior knowledge, real-world applications often involve uncertain or imperfect initial distributions. |
No matching items