Risk-averse Bayesian Optimal Experimental Design
This project addresses a fundamental challenge in BOED: the sensitivity of experimental outcomes to misspecified prior distributions. While traditional BOED methods assume accurate prior knowledge, real-world applications often involve uncertain or imperfect initial distributions.
To tackle this challenge, we developed Risk-averse Expected Information Gain (REIG), a novel approach that accounts for prior uncertainty while maintaining computational efficiency. Our method leverages convex optimization techniques to: - Minimize the risk associated with prior misspecification - Ensure robust experimental designs that perform well across a range of possible prior distributions - Maintain computational tractability through efficient convex optimization algorithms
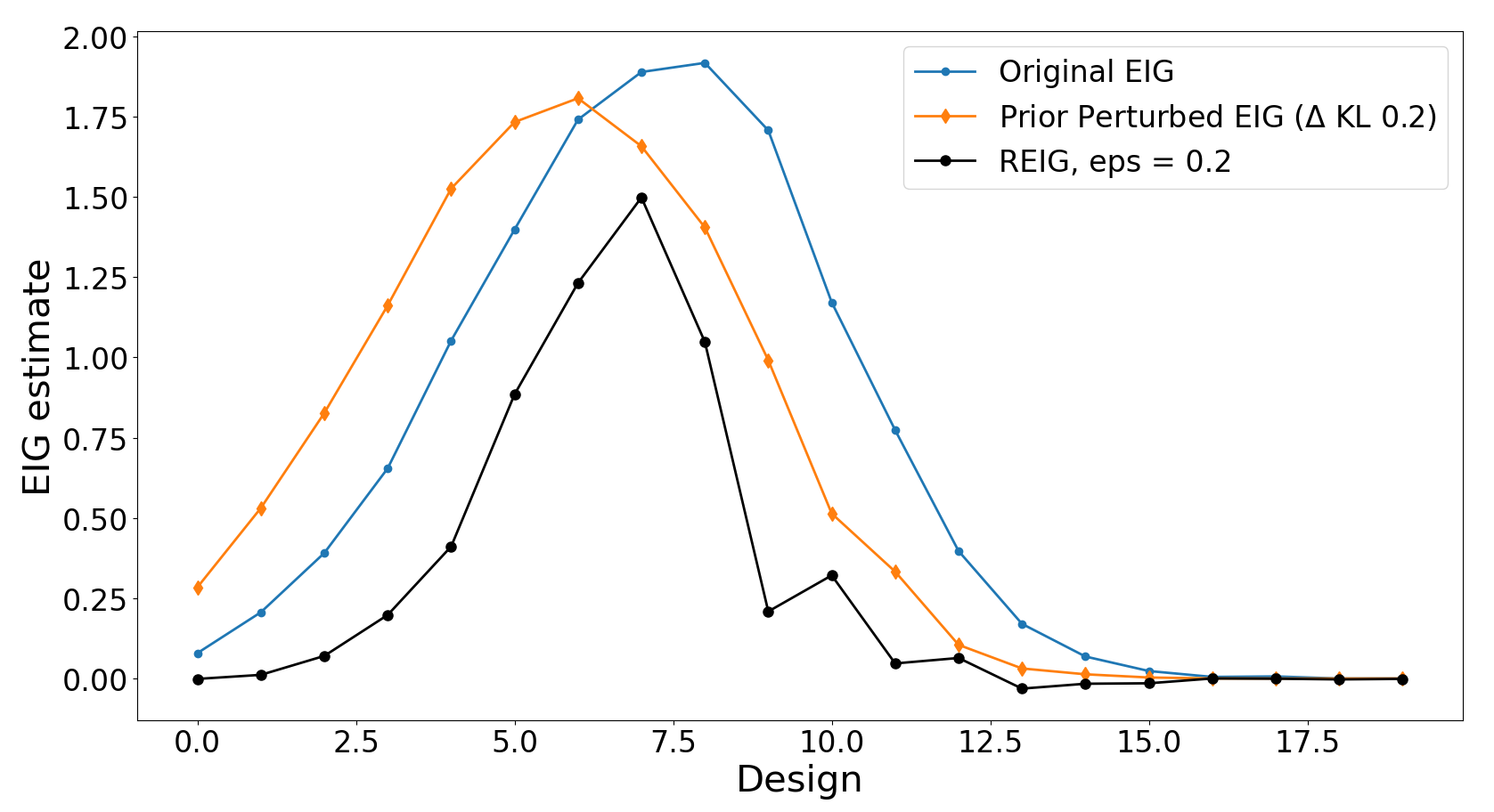
The accompanying visualization demonstrates how changes in the prior distribution can significantly impact the optimal experimental design, highlighting the importance of accounting for prior uncertainty.
Our framework integrates seamlessly with existing convex optimization methods, providing a practical solution for real-world experimental design scenarios where prior knowledge may be incomplete or uncertain.
Publication: Go, J. and Isaac, T. (2022). Robust Expected Information Gain for Optimal Bayesian Experimental Design Using Ambiguity Sets. Proceedings of the 38th International Conference on Uncertainty in Artificial Intelligence