Bayesian Optimal Experimental Design with Neural Operators
Neural operators have emerged as a powerful tool for learning mappings between function spaces, with direct applications to PDEs. These operators provide an elegant solution to reduce the computational burden of infinite/high-dimensional PDE solvers. Through their application in BOED, we’ve developed two approaches:
DINO (Derivative-informed Neural Operator)
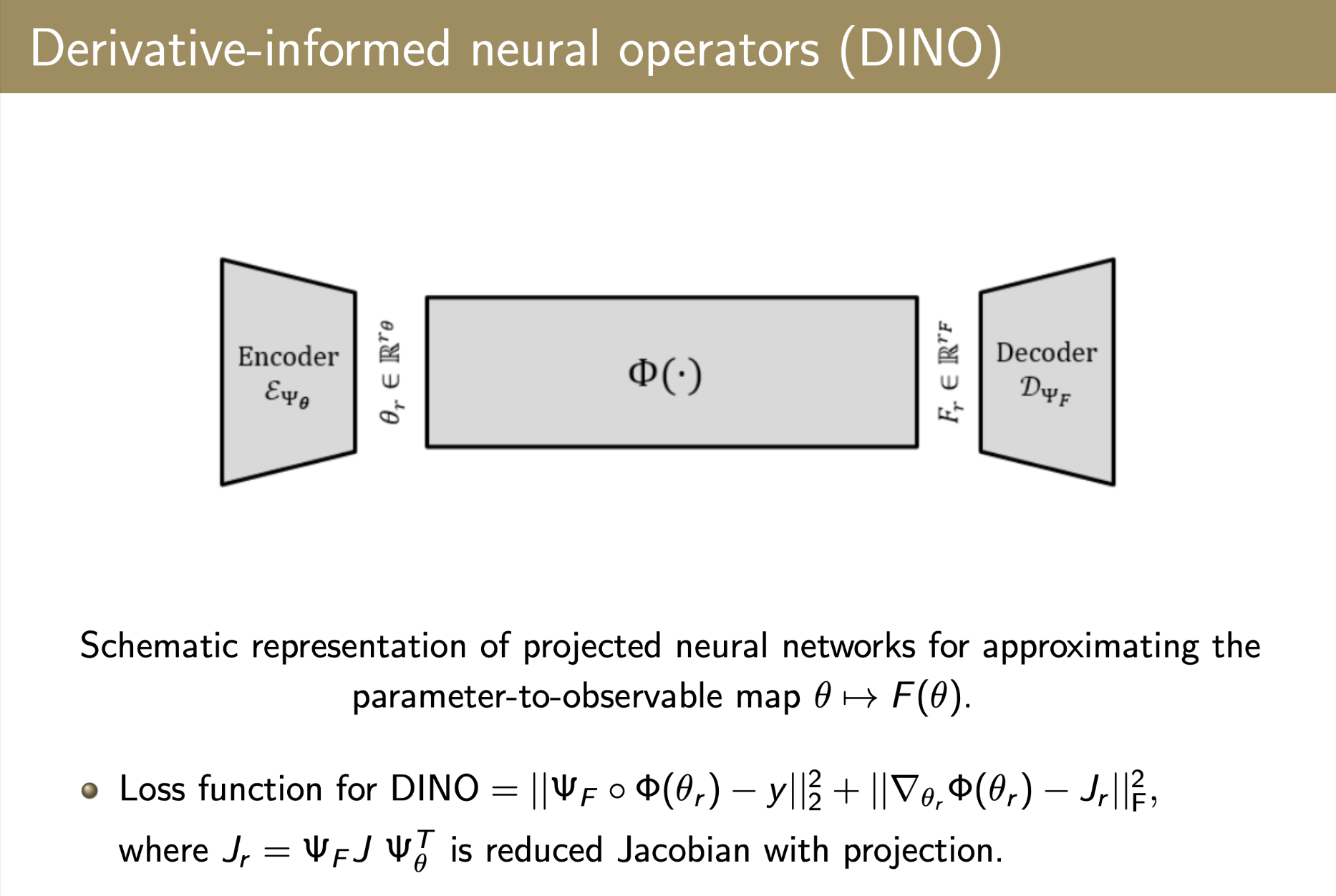
DINO incorporates derivative information. We’ve trained a model that achieves superior accuracy in both parameter-to-observable maps and their corresponding Jacobians. Key features include:
- Efficient surrogate modeling for time-independent PDEs
- Dramatically reduced computational costs while maintaining high accuracy
Our comprehensive analysis and theoretical foundations are detailed in our paper:
Accurate, scalable, and efficient Bayesian optimal experimental design with derivative-informed neural operators
LANO (Latent Attention Neural Operator)
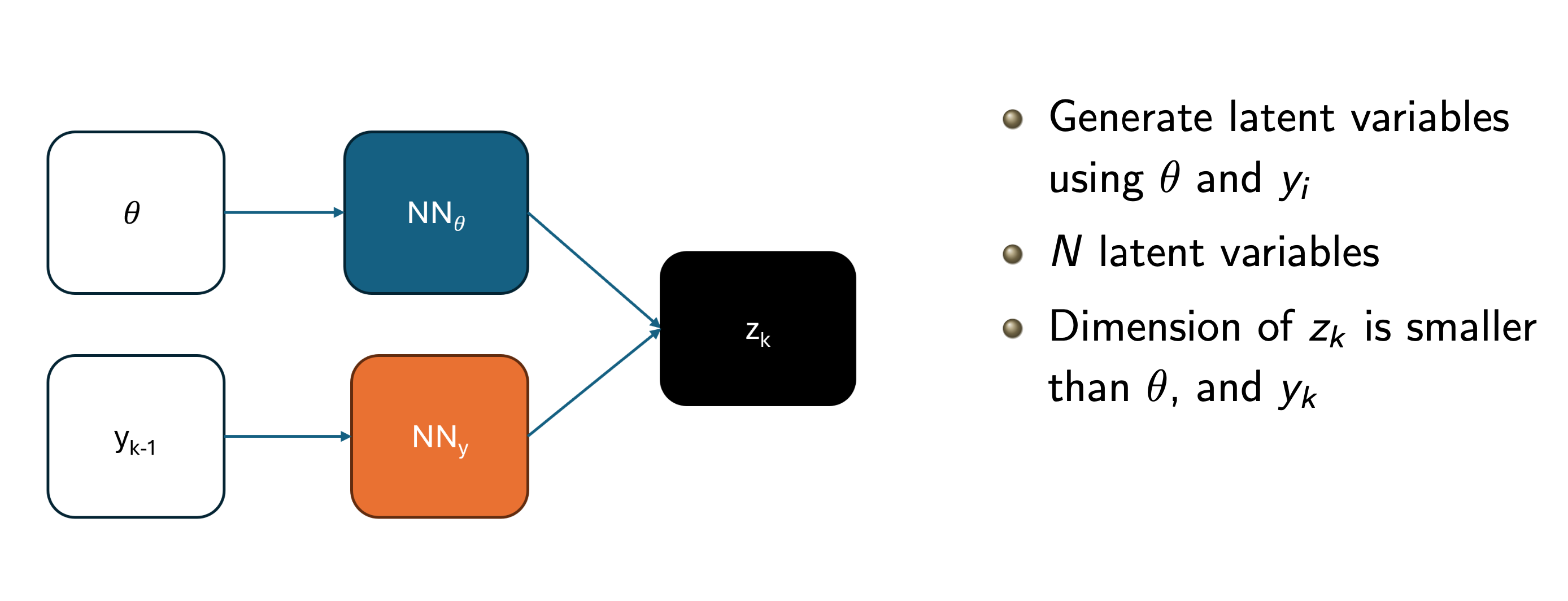
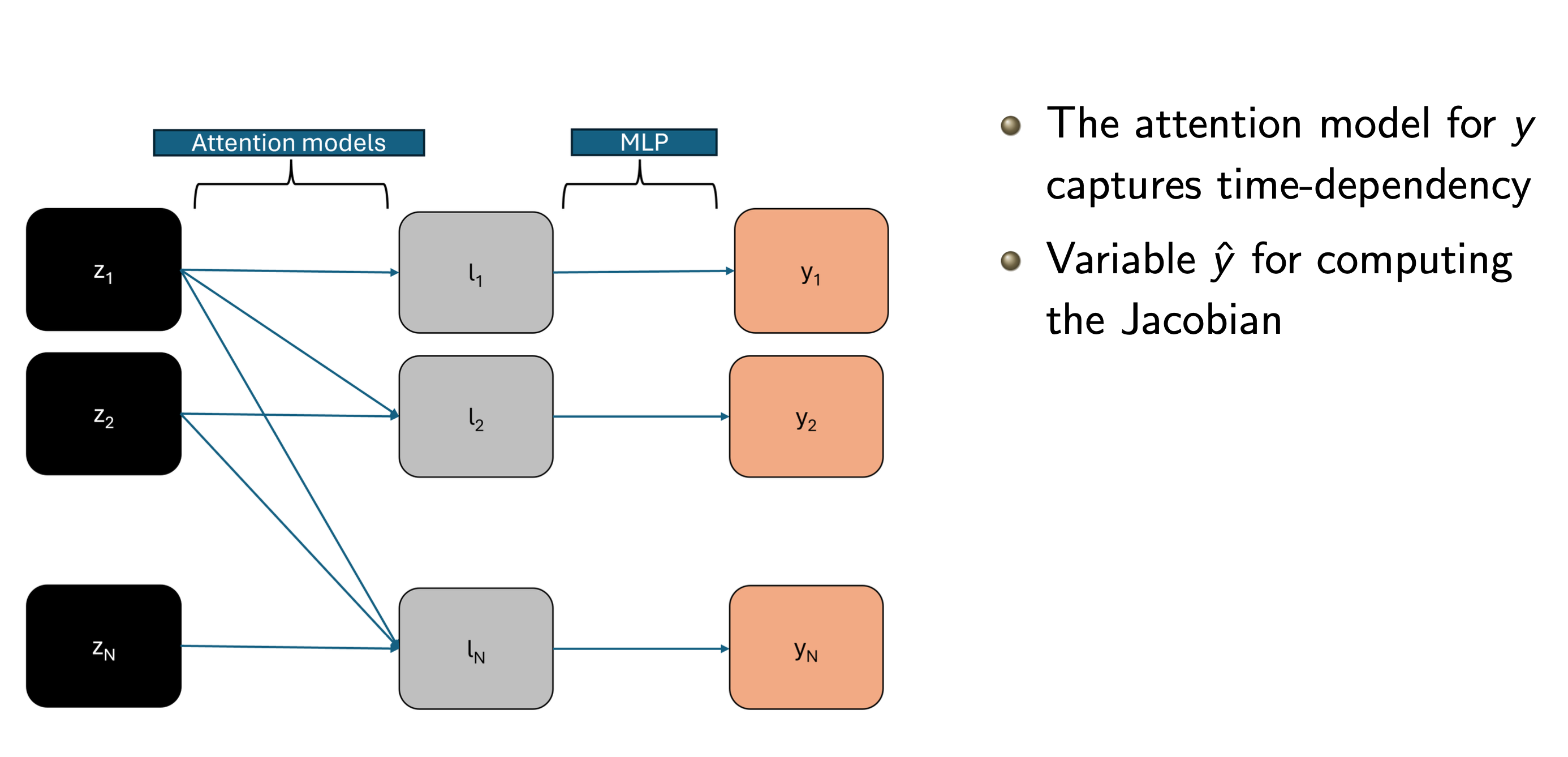
Building on the success of DINO, we developed LANO to address the challenges of sequential Bayesian optimal experimental design. This architecture introduces several innovative features:
- Advanced latent attention mechanism for handling complex temporal dependencies
- Efficient optimization methods for sequential experiments
The theoretical framework and experimental results are extensively documented in our paper:
Sequential infinite-dimensional Bayesian optimal experimental design with derivative-informed latent attention neural operator