Bayesian Optimal Experimental Design
In research settings where experiments are expensive, time-consuming, or potentially hazardous, it’s crucial to optimize experimental design to maximize information gain. This research advances Bayesian optimal experimental design (BOED) methodology to address these challenges.
Approaches
BOED has employed several key methodologies:
Gaussian Approximation Method
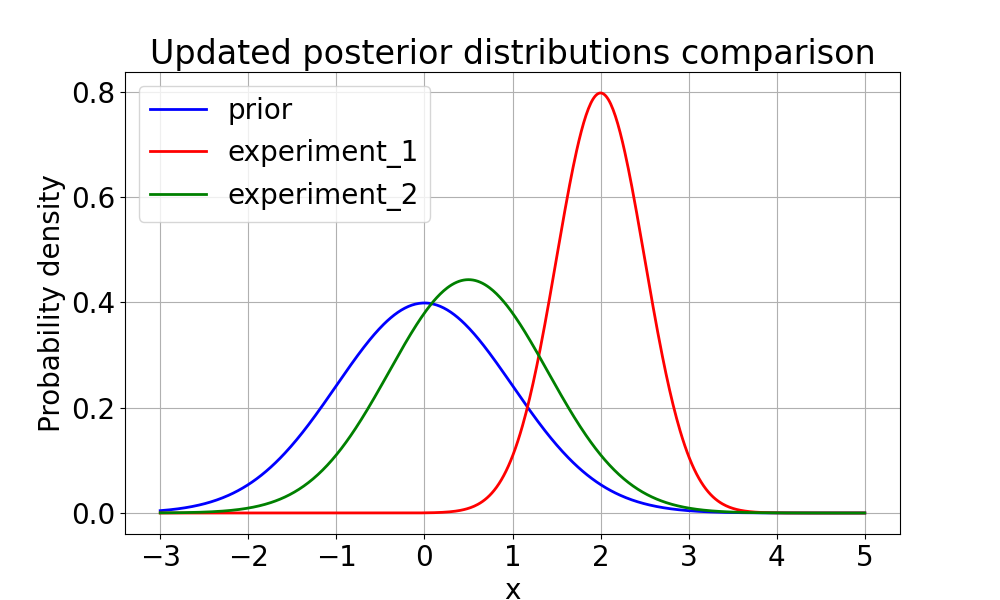
This approach leverages Gaussian approximations of posterior distributions to evaluate uncertainty reduction through posterior covariance matrices.KL Divergence Method
This method involves calculating the expected Kullback-Leibler (KL) divergence between posterior and prior distributions to quantify information gain.
While these approaches are theoretically sound, they often involve significant computational overhead, limiting their practical application.